There’s been a lot of talk about false positive and false negative rates lately, especially with Covid testing being so widespread. If you receive a negative Covid test with a 90% false negative, does that mean that you only have a one in ten chance of actually having it?
This week I want to dive into the world of probability with an easy-to-understand and hard to believe example that will likely trick most people. It’s called conditional probability and it’s perplexed people for a long time.
I’ll use a little math, but bear with me and we’ll have a bit of fun with probabilities (yes, that can actually be a thing) that, for the uninitiated, will give you a good appreciation for the professional practitioners who need to get this right every day.
Let’s get started
But first some quick definitions in the case of health:
- False positive – a test reveals a person has a particular condition, but the person does not actually have the condition
- False negative – it’s the opposite; the person is told they don’t have a condition, but the person actually has it
Which is worse? As always, it depends.
A false positive (such as proclaiming a person has some disease) can be emotionally devastating. At large scale, it can cause the unrest of entire communities. Imagine a false claim that a sewage spill has contaminated a waterway, or that a particular farm is distributing food laden with E. coli.
A false negative generally has its own set of challenges; imagine not detecting a disease in an early stage where it can be treated effectively. Or imagine not detecting E. coli in a food distribution plant. And more recently with Covid, imagine trusting people who recently received a negative Covid test, only to find out that the test had an unacceptably high false negative rate.
Would you feel comfortable spending time with that group of people?
Let’s look at how these false/true positive/negative results can occur in something we call a contingency table:
Let’s make up some numbers and see what the implications are of getting tests wrong. For this, we’ll need to make up some dummy data.
Say we have a test where the true positive rate is 90%. In other words, when the test comes back positive, it’s correct nine out of ten times. And let’s say the false positive rate is 5%, so when the test says positive, it’s wrong 5% of the time.
Refilling the contingency table, we have:
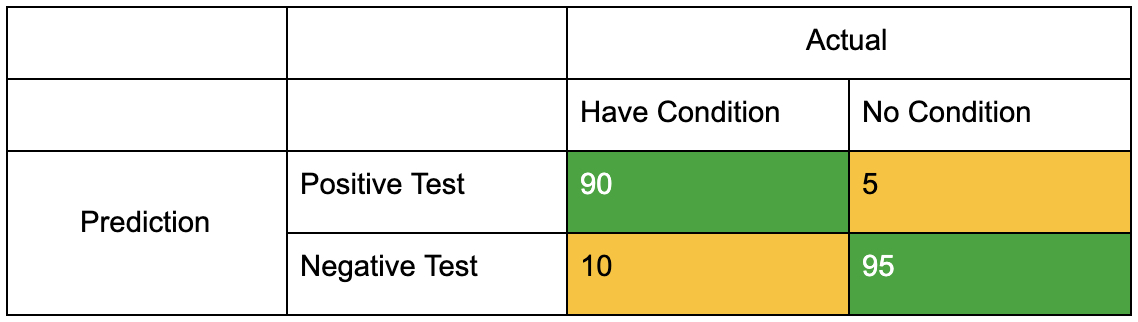
Let’s pretend the table above describes some condition named ABC syndrome. And let’s also assume that 2% of the population has this condition.
Now that we have all this information, can you answer this question?:
If a person tests positive for ABC syndrome, what’s the probability that the person actually has the condition?
Really, think of a percentage before you read on. Maybe 75%? 90%?
This next part gets technical! Skip it if you want…

Conclusion
The answer is = 27%
Again, that’s the actual probability that the person actually has the condition given that the person tests positive for ABC syndrome.
How does that answer compare to your guess? How could it be so low when the true positive rate is so high?
Conditional probabilities cause big swings in actual probabilities and deserve a lot of respect. Often, it’s not enough to have a gut feeling about numbers, especially when this sort of thinking is well outside our day-to-day.
The take-home is that it’s important to consider factors outside single numbers. It’s important to consider other conditions.
I’ll leave you with food for thought and ask you the same question again: If you receive a negative Covid test with a 90% false negative, does that mean that you only have a one in ten chance of actually having it?
Have a healthy week!
-Zank
Of Interest
Sick of Traffic Jams? A.I. may Come to the Rescue
It’s hard to think of a single upside to sitting in traffic. The downsides? Stress. Loss of productivity. A waste of gas. Did we mention stress? Artificial intelligence may be coming to the rescue. Six years ago, the city of Pittsburgh collaborated with Carnegie Mellon University to develop adaptive traffic control signals in a section of town that was plagued by terrible traffic. The program put artificial intelligence to work to analyze the traffic flow throughout the day—and change the signals when it makes sense instead of on a predetermined schedule. Curious? Read more here.
Predictive Policing” in its Purest Form
Chicago’s predictive policing program told a man named McDaniel he would be involved with a shooting. But it couldn’t determine which side of the gun he would be on. When the police informed him, McDaniel didn’t know how to take the news. The idea that a series of calculations could predict that he would soon shoot someone, or be shot, seemed outlandish. But the visit set a series of gears in motion and this Kafka-esque policing nightmare — a circumstance in which police identified a man to be surveilled based on a purely theoretical danger — would seem to cause the thing it predicted, in a deranged feat of self-fulfilling prophecy. Read more here.
Germany Gives Greenlight to Driverless Cars on Public Road
Germany has adopted legislation that will allow driverless vehicles on public roads by 2022, laying out a path for companies to deploy robotaxis and delivery services in the country at scale. While autonomous testing is currently permitted in Germany, this would allow operations of driverless vehicles without a human safety operator behind the wheel. Read more here.
