A/B testing is such an important step in product development because it’s directly tied to revenue.
by: Zank, CEO of Bennett Data Science
Big data-driven companies know this. They run thousands of tests concurrently! They have teams that develop in-house systems for monitoring all these tests. It’s a massive part of their life blood. And for good reason: data science models and product enhancements can’t be considered improved unless they’re measured. And A/B testing is how that’s generally done. But like anything else, some companies get it right, and some don’t.
It’s really easy to waste a lot of time and resources on A/B testing. In this post, I’ll explain how typical A/B tests are performed, what they’re designed to do and show you how to make tests work for, not against your business.
And if you’re not yet testing, there’s no better time to start than now! Call us, we can help. After all, what gets measured gets managed, and A/B tests are ultimately just powerful measurement tools. (See part two of this article for a rundown of types of A/B tests and which perform best.)
I’ll assume you’re on board with the importance of testing. I’m glad that’s out of the way! For the rest of this post I’ll show you how to think about efficient testing. Testing that gives you the answers you need, quickly and automatically. First, we’ll look at how we usually see companies approach tests, then we’ll dive into a newer and more efficient method that can save you a lot of valuable time and money (i.e., impressions). Let’s dive in!
Here’s what typical A/B tests look like:
Let’s consider a very simple example: we have one product to show to customers who visit our website. Let’s say we’re selling bicycles. So, we dream up this landing page. We love it but can’t agree on the text. A perfect opportunity to A/B test. We’ll call A, “Bike to Work”, and B, “Win the Race”:
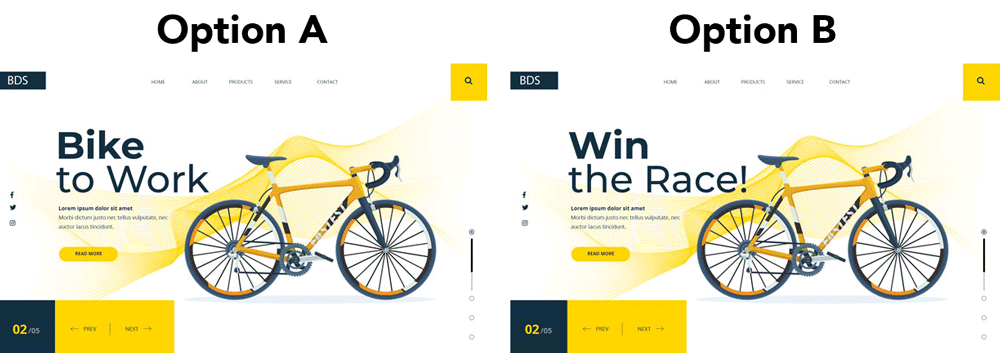
A/B tests generally require that we show option A to a lot of users and option B to different users. Then, after A and B have been shown to a LOT of users, we look at the numbers and say that A performs better than B. There are some details, like p-values and confidence intervals to consider. I won’t get into these here, but there are a few important details to this type of A/B testing:
- We must show each image a certain number of times. For an ad like this, we would probably need 1,500 impressions each. That’s 3,000 views before we can pick a winner
- We can’t look early and just end the test if one ad seems to be “winning”. You can’t. It invalidates the entire test. Bad bad, dark dark day.
Let’s look at what’s wrong with this typical A/B testing approach:
- It can be very wasteful; If most everyone in our user demographic bikes to work and doesn’t race, then we’re wasting most of the 1,500 impressions going to that ad. And we know how expensive impressions can be.
- There’s no peeking allowed. We don’t know anything until the test is done. It’s like there’s nothing learned until there IS. There’s good math behind why, but something just feels wrong with this; something begs for a better way!
Here’s Evan Miller to dive in a bit deeper and explain it perfectly:
If you run A/B tests on your website and regularly check ongoing experiments for significant results, you might be falling prey to what statisticians call repeated significance testing errors. As a result, even though your dashboard says a result is statistically significant, there’s a good chance that it’s actually insignificant.
OK, you’ve probably heard that before. But still, there must be a better way, where we can learn from each user visit (click) and get smarter as we go.
Wasting impressions is no fun and works against your business. So, in this document, We’re going to show you how you can do something much smarter, much faster, so you can stop wasting time and money on tests and spend more time doing what you’re best at: building great products!
The Multi Armed Bandit:
What if I told you there was another method that works in many cases, but that doesn’t require you to wait? At all! What if I told you there’s a method that automatically shows more of the winning option as soon as it starts winning?
We actually have something that does just that. It’s called the Multi Armed Bandit with Thompson Sampling. That’s a mouthful, so I’ll just call it the MAB (for Multi Armed Bandit) from here on out.
It’s worth taking a moment to explain the name.
Let’s imagine you have a room with 5 slot machines, where each machine pays out at a fixed percentage of the time. You also have a bucket full of coins. How do you maximize your winnings?
This is the multi-armed bandit problem
The best strategy is to spend some time trying each machine (exploring) to see which one seems to be paying off more often, then playing (exploiting) the machine with the highest pay-off. But while playing (exploiting) the best payout, there’s still a chance that another machine would perform better, so the temptation is to wander around a bit more, trying the machines a bit more (exploring).
When should we stop? When have we explored enough to be confident that we can exploit the heck out of the one big-money machine? This is called the explore-exploit tradeoff dilemma and it’s exactly what the MAB algorithm solves for us! You can read a lot more about it here. This is also happens to be what Google uses for its experiments. They provide a great technical overview of A/B testing with multi-armed bandits. It’s a very well written article and I highly recommend reading through all the pages to get a good background.
In the rest of this article, we’ll show you why to use a MAB, when you should use one, and exactly how to implement one. Let’s get to it!
Why should you use a MAB?
Let’s paint an even bleaker picture of that first type of A/B testing (called the frequentist method). First we pick a null hypotheses, something like, B will not perform better than A. Then we pick some statistics significance we need to achieve (are you sleeping yet?). Call it 95% confidence. Then we need to run the experiment with, say 1,500 impressions per each option. If we have more than two options, things get much worse, and with four or five options, you could be running the test for YEARS to get enough impressions. Really, years! That costs money. Why? Because if one of the options is a dog, you’re losing money every time it’s shown or used! We can do better.
In summary:
Frequentist A/B testing:
- Can be complicated to understand and set up
- Requires many impressions before an answer is known, and is generally wasteful
- Requires an insane amount of impression for the case of four or five options
In contrast, let’s look at the MAB
- They require no set up or pre-planning
- They’re self adjusting, minimizing wasted impressions and maximizing revenue
- They work just as well on many variations (A/B/C/D) as they do on two (A/B)
In addition, MAB’s are extremely lightweight, as you’ll see later on in Implementation
How do they compare?
Let’s run an experiment. Let’s go back to our two landing pages, A and B. And since this is a thought experiment, let’s say we have lots of users, just waiting to see them.
We’re going to run a usual (frequentist) A/B test and the MAB (probabilistic) A/B test. You don’t have to do a thing. Just wait right here; I’ll fire up Python and run this experiment.
Here are the details:
Typical A/B:
For this method, the first thing we need is the number of times to show A and B each. So, we go to this page and see that for the given criteria, we need to show each variation 1,600 times! (I had underestimated. It’s worse than I thought!)
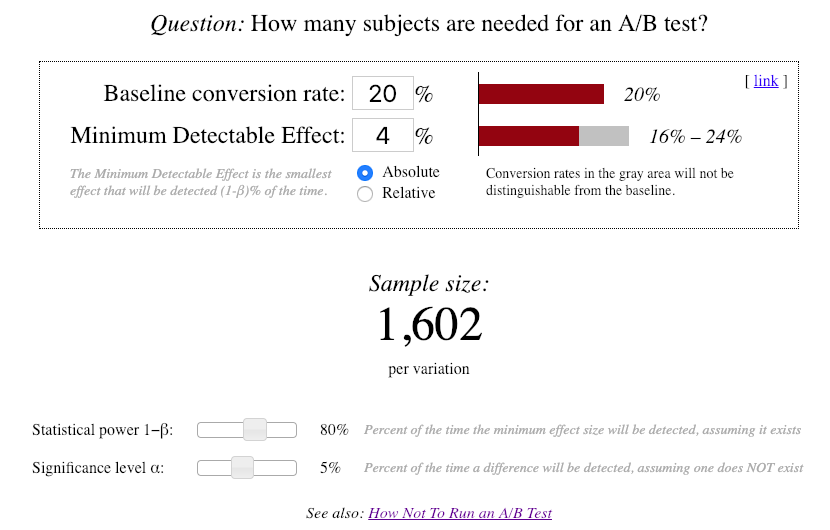
So in my simulation, I’ll show A to 1,600 people and B to 1,600 people.
To keep things fair, I’ll send 3,200 (1,600 + 1,600) impressions through the MAB.
We’ll assume that impressions cost us $1.00 each and that landing page A has a click-through rate of 45% and page B has a click-through rate of 10% (remember, these are bike commuters, not racers, so we don’t expect many to click on version B with the racing copy)
At the end, we expect to waste some money by showing impressions of B, when A is clearly the better option, since its click-through rate is 35% higher.
Now, please put your feet up and make yourself at home while I turn the crank on the machine…
OK, I’m back with the results:
I ran each of the A/B tests 1,000 times. In other words, I fed each machine all 3,200 users, 1,000 times. On average, here’s how each did interns of leads and return on investment.
CASE 1: The first case is trivial to compute. Since nothing can change, we can simply state that:
- Total cost to run test: $3,200.00
- Version A got 720 clicks. Version B got 160 clicks
- Cost per click: A: $2.22, B: $10.00
- Regret (of having ever showed B) is: 560 clicks (720 – 160)
Take-home: If we had shown version A every time, we would have received 560 more clicks! But remember, we had to go through 3,200 clicks to get to this conclusion confidently.
That number, 560, is called our regret. Bluntly, regret is how much we lost by showing the “bad” option. It’s defined as the total possible reward minus the observed reward. Since we can peer behind the curtain, we know that showing all 3,200 users option A would have had a 45% click through rate, or 1,440 clicks. Our regret is just 1,440 minus the actual number of clicks.
560 lost clicks is pretty severe. Clearly we want to minimize the regret of showing the wrong option. MAB’s are designed to do just that. Let’s take a look at case 2 and see what the MAB can do!
CASE 2: The multi-armed bandit requires a simulation environment. In this environment, we show each ad until a winner is chosen by the algorithm, then we stop the test since we have a winner. In this case a winner is the bike ad, A or B, that we want to show for the rest of the experiment. I simulated this by running the experiment 1,000 times. Here’s are the results:
- Percent of times we computed the winner correctly at time of stopping: 99.4% (994 of 999)
- Out of 1,000 trials, the average number of impressions to find a winner was 54.9 impressions
- Out of 1,000 trials, A & B were shown an average of 46.7 and 8.2 times, respectively
- Average number of missed clicks (from showing the wrong option) (our regret): 4
Wow, that’s a HUGE difference. We’re wasting, on average, only four clicks! CASE 1 was wasting 560 clicks. That’s a difference of 556 potential customers!
This is exactly why MAB’s are so lauded.
As with any testing platform, be there are some important things to remember when using MAB’s
MAB’s work really well when our pool of users is consistent. It might be obvious, but if in the middle of our 3,200 user study we suddenly change our marketing channel (say, to bike racers who don’t commute), it drastically alters the underlying assumptions. In this case, it’s best to stop the experiment and re-start with a clean slate for this new demographic. The take-home here is, any time user demographics will vary widely, make your data professionals aware of the changes!
Conclusion
We’ve seen how the MAB algorithm can outperform standard statistical A/B tests. And for A/B/C/D, etc tests with lots of options, in some cases standard tests won’t finish for years, where a MAB would converge in days. MAB’s are:
- Simple to implement
- Useful when you don’t know much or anything about your audience
- Easy to interpret results
- Very efficient in terms of computational resources (lower your EC2 bill!)
- Self organizing, so you don’t choose a winner, it does it for you
But, MAB’s:
- Can be somewhat difficult to understand and explain to a broad audience
- Aren’t the best choice when there is a lot of information known about your users
- Aren’t the best choice when you need to understand why certain variants did or did not perform
Still hungry for more?
Ready for more? Here’s part two, where we discuss the most effective methods for A/B testing using MABs.
References:
The Smart Marketer: When to Use Multi-Armed Bandit A/B Testing: https://www.retentionscience.com/blog/multi-armed-bandit/
Overview with Simulation and Python code: https://github.com/zankbennett/multi_armed_bandit_tech_overview/blob/master/MAB%20Talk%20-%20Bennett%20Data%20Science.pdf
Zank Bennett is CEO of Bennett Data Science, a group that works with companies from early-stage startups to the Fortune 500. BDS specializes in working with large volumes of data to solve complex business problems, finding novel ways for companies to grow their products and revenue using data, and maximizing the effectiveness of existing data science personnel. https://bennettdatascience.com
